Exploring the Synergy of Riemannian Optimization and Manifold Learning in AI
In the dynamic world of artificial intelligence, the intersection of Riemannian optimization and manifold learning is revolutionizing machine learning practices. By embracing the intricacies of geometry, researchers can tackle complex, high-dimensional datasets more effectively.
Key Insights:
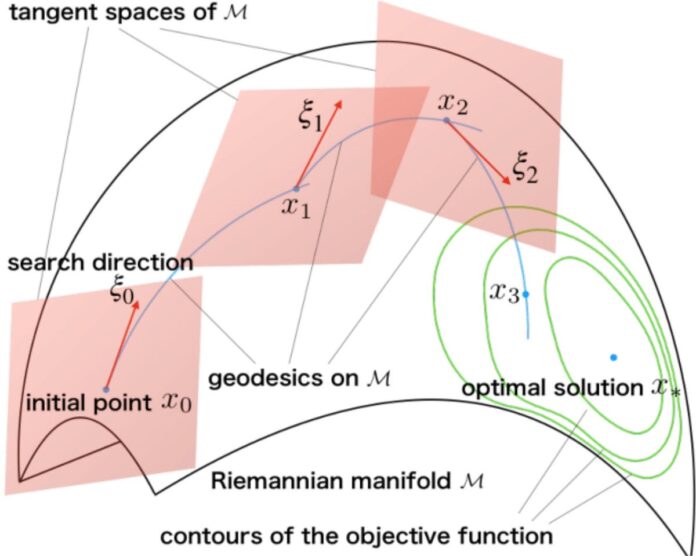
- Riemannian Optimization:
- Evolves classical optimization to operate on non-Euclidean manifolds.
- Ensures geometric constraints are respected, leading to enhanced accuracy and faster convergence.
- Manifold Learning:
- Discovers hidden low-dimensional structures within high-dimensional data.
- Nonlinear methods like Isomap and t-SNE enable insightful data representation and visualization.
Combined Benefits:
- Leveraging geometric structures leads to smarter neural network training and robust dimensionality reduction, enhancing algorithms across computer vision and signal processing.
- Adoption of these techniques is increasing, supported by a growing ecosystem of tools and resources, making them more accessible for practitioners.
As these areas continue to expand, the synergy between Riemannian optimization and manifold learning will redefine how we perceive data geometry in machine learning.
👉 Join the conversation! Share your perspectives on the future of geometry-aware AI.