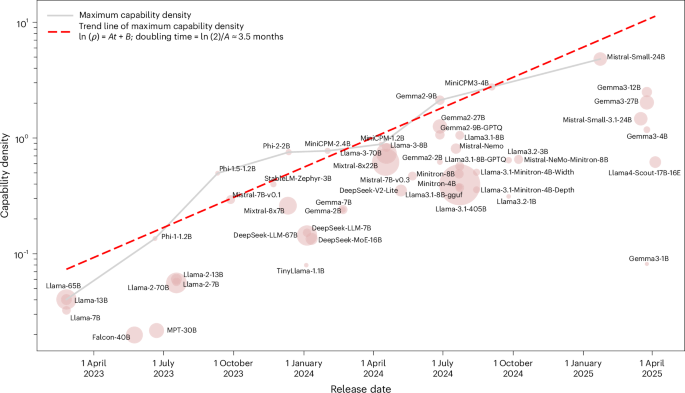
In this content, we define the density of large language models (LLMs) as the ratio of effective parameter size to actual parameter size. We start by establishing a framework to estimate effective parameter size through scaling laws, focusing on the relationship between parameter size and model performance on downstream tasks. Using fitted functions, we derive the effective parameter size that a reference model would need to match a given model’s performance, with density calculated as \(\rho ({\mathcal{M}}) = \frac{\hat{N}({S}_{{\mathcal{M}}})}{{N}_{{\mathcal{M}}}}\).
We detail a two-step estimation process for loss and performance, incorporating conditional loss calculations tailored to various task formats. We explore capability density for both dense and efficient LLM architectures, including sparse MoE and quantized models, emphasizing how parameter size relates to computational efficiency, inference time, and performance. The content highlights models like Llama, Falcon, and others, analyzing density trends and evaluating them based on established datasets. This comprehensive analysis aims to improve LLM performance while considering computational constraints efficiently.
Source link